A new article on discrete integrable systems associated with relativistic collisions is published in Physica D: Nonlinear Phenomena.

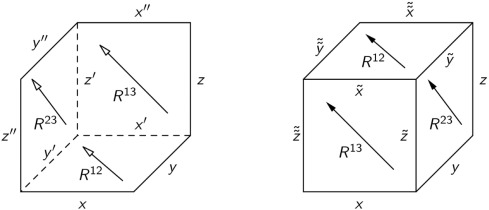
Abstract: We study vector quadrirational Yang–Baxter maps representing the momentum–energy transformation of two particles after elastic relativistic collisions. The collision maps admit Lax representations compatible with an r-matrix Poisson structure and correspond to integrable systems of quadrilateral lattice equations.

TE Kouloukas, Discrete integrable systems associated with relativistic collisions, Physica D: Nonlinear Phenomena, 456, 2023, https://doi.org/10.1016/j.physd.2023.133937